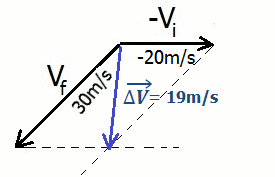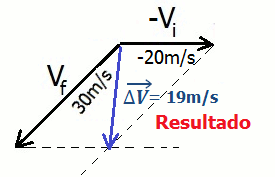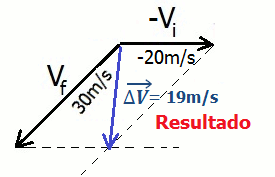
Ainda em relação à subtração vetorial, imagine uma bola com velocidade inicial vi (20m/s) que após ter recebido um chute, passa a ter uma velocidade final vf (30m/s), em outra direção.
Em relação à variação de velocidade da bola, o oposto da velocidade inicial vi, é:
Desse modo,
Pelo método do paralelogramo, teremos:
Para determinar o módulo de ΔV usamos a lei dos cossenos:
Se usar um transferidor e medir o ângulo θ, encontrará aproximadamente 140o, assim:
Outra forma de se realizar a diferença entre vetores
Retomemos a diferença entre as velocidades que fizemos anteriormente. A bola com velocidade inicial vi (20m/s) recebe um chute e, passa a ter uma velocidade final vf (30m/s), em outra direção.
Ao invés de realizarmos a subtração vetorial pensando numa soma vetorial, usando o vetor oposto a vi (-vi):
Podemos fazer da seguinte forma:
Resumindo, imagine dois vetores v1 e v2 com um ângulo α entre eles:
A soma entre eles é:
(método do paralelogramo)
A diferença entre eles é:
1o - Colocamos a origem dois dois vetores (vi e vf) em um mesmo ponto, como se fôssemos somá-los pelo método do paralelogramo:
2o - O vetor diferença ΔV é simplesmente o segmento que liga as pontas dos vetores, e seu sentido aponta para o vetor minuendo, nesse caso, vf :
3o - O módulo do vetor diferença ΔV é calculado através da Lei do Cossenos, mas com duas diferenças, o termo onde aparece o ângulo entre os vetores recebe o sinal de menos, e o ângulo agora é suplemento (α) daquele usado no método anterior (θ):
Resumindo, imagine dois vetores v1 e v2 com um ângulo α entre eles:
A soma entre eles é:
(método do paralelogramo)
A diferença entre eles é:
Entendeu? Então vamos continuar?
Clique aqui para continuar.
8